Notação de Dirac- Quantum Bit

                            ;
                               

"What would the situation be if our computer is operating according to the laws of quantum mechanics?" Richard Feynman

Sempre busco na web material que me auxilie na composição de minhas postagens e que tragam subsídios para assuntos aos quais estou interessado em aprender e desta maneira, adquirir alguma intimidade com os mesmos durante minhas navegações, pois afinal, meu lema é navigo et adaperio.

No caso, a mecânica quântica é um dos assuntos que me fascina e mais especificamente, a computação quântica é um assunto que me interessa profissionalmente, e por isto, sempre busco na web algo que tenha sido publicado e que seja inteligível para mim.

Em uma dessas buscas deparei com o artigo acadêmico UMA PROPOSTA DIDÁTICA PARA O ENSINO DE MECÂNICA QUÂNTICA NAS LICENCIATURAS : a notação de Dirac de autoria de Marina Valentim Barros, que veio ao encontro de minhas necessidades para entender tal assunto, além, de proporcionar um panorama bastante realista sobre o ensino da Física Moderna no Brasil, também serviu de referência para esta postagem, assim como outros artigos ou livros que mencionarei ao longo do texto.

Texto que começo com a asserção contida na introdução do referido artigo que diz: [...] A utilização do formalismo de Dirac na mecânica quântica é usual em áreas que trabalham com esse assunto.

Porém, mesmo em áreas em que a mecânica quântica não é utilizada como ferramenta imediata essa linguagem é usada.

Esse formalismo é utilizado em cursos de formação de professores, em cursos de alunos do ensino médio interessados em estudar a mecânica quântica, em cursos introdutórios de computação quântica e servindo até mesmo de linguagem para livros de divulgação científica dirigido ao publico leigo.

Uma experiência de utilização desse formalismo é um trabalho proposto por Greca, Moreira e Herscovitz para ser aplicado em disciplinas introdutórias de mecânica quântica, defendendo a notação de Dirac como facilitadora e simplificadora,

“Em relação às ferramentas e simbolismo matemáticos utilizados, escolhemos trabalhar com a ágil notação de “bras” e “Kets” de Dirac. Embora não usual para os estudantes do grupo em foco, a notação não foi um impedimento para a compreensão dos alunos.

Ao contrário, uma vez aceita como outra forma de denotar vetores de estado, tornou-se de grande utilidade na discussão, por ser compacta e rica.” (GRECA;MOREIRA;HERSCOVITZ ,2001,p.2) (os destaques são de minha autoria.)

Considerando que na área da computação o assunto é obviamente assaz pertinente, em face ao alto desenvolvimento da capacidade computacional advindo de novas técnicas e também na eletrônica por novos desenvolvimentos no hardware, recorro ao trabalho acadêmico de Pamela Polnow Gnutzmann que no inicio relata: :

“Atualmente, observa-se uma grande redução no crescimento de desempenho dos processadores clássicos. 
Sua capacidade de crescimento quase exponencial, prevista por Gordon Moore em 1965  

                                     

                                                                

                                        Moore’s Law. Source: Intel.
                                                     (MOORE, 1965),

está atingindo limites físicos, como latência de memória, dissipação de energia e tamanho mínimo de transistores usados, para manter um sistema eletrônico livre de ruídos.

Em busca de contornar tais limitações surgem novos paradigmas de computação como a Computação Paralela e Distribuída, a Computação Natural e a Computação Quântica (CQ), que substituem as técnicas utilizadas nos paradigmas atuais.

Sendo fundamentada nos postulados definidos pela Mecânica Quântica (MQ), a Computação Quântica (CQ) aplica propriedades físicas aí estabelecidas para a concepção de uma nova classe de computadores (quânticos), que podem apresentar um desempenho exponencialmente melhor que os computadores clássicos na computação de determinados problemas.

Devido à extrema complexidade dos fenômenos previstos pela MQ e a grande dificuldade que se encontra na interpretação e desenvolvimento de algoritmos quânticos, se faz necessário o uso de ferramentas e modelos que auxiliem essa aprendizagem”.(os destaques de minha autoria)

Em vista de tal contexto. fica patente que o conhecimento de tal ferramenta desempenha

importante papel para o domínio das novas tecnologias e conforme tomei ciẽncia, é um

 conhecimento centenário, haja vista, vem do trabalho do físico Niels Bohr lançado em 

1913 referente ao modelo atomico, sendo que Bohr é considerado um dos principais

 arquitetos do átomo e da física quântica!

 

Outros físicos como Erwin Schrödinger que nasceu em 1887, na cidade de Viena na 

Àustria, e em 1926 publicou os artigos que lhe deram o título de fundador da mecânica

 quântica, pois, propôs uma equação conhecida como função de onda para a explicação da 

dualidade  onda-párticula.

                                             

A equação acima foi obtida pela primeira vez em 1926 por Erwin Schrödinger e é, portanto,

 chamada de equação de Schrödinger. 

Esta equação descreve a evolução temporal e espacial de um estado quântico de um 

sistema físico, tendo uma grande importância na mecânica quântica.

Outro importante cientista a contribuir para a consolidação desta nova teoria foi Paul Dirac

 autor do assunto em questão.

                                        

Este nasceu em 1902, na cidade de Bristol, na Inglaterra, e publicou em 1928 importantes

 trabalhos sobre a teoria quântica relativística do elétron e a previsão de existência das

 antipartículas. Em 1933, Schrodinger e Dirac dividiram o cobiçado prêmio Nobel de Física 

e são reconhecidos como dois dos maiores cientistas da física moderna. 
 

A notação de Dirac proposta por ele no seu livro," Os princípios da mecânica quântica “, de 1930, que garante uma elegância ao tratamento formal da mecânica quântica associando aos estados quânticos, grandezas semelhantes a vetores.

Que de acordo com Richard Feynman, “Tudo o que faremos na mecânica quântica pode se feito com álgebra linear simples e essa nova maneira é simplesmente uma forma de escrever a mesma coisa de forma diferente.  
Sabendo essa nova notação você será capaz de entender o que as outras pessoas dizem. Quando as pessoas trabalham a mecânica clássica estão acostumadas a tratar todas as equações em termos das componentes x, y e z e alguém mostrou que escrever isso em forma de vetores facilitaria o trabalho.

O que faremos na mecânica quântica é escrever as grandezas usando o conceito de um vetor de estado”. (FEYNMAN, 1968, p 20.1). destaques são de autoria do blog.

O uso e a compreensão da notação torna-se importante em função do avanço tecnológico e da observação do fato, que no que concerne à tecnologia digital há uma convergência em direção a mecânica quântica, tanto computacional através dos algoritmos, quanto física pelo advento de novos componentes.

Então, é justificada minha tentativa em tentar entender tal notação e compartilhando este entendimento, reforço os conceitos, pois, a regra do aprendizado significativo é, segundo Ausubel (citado pela autora do artigo), escrever o que foi aprendido com suas próprias palavras dando significado pessoal ao que foi compreendido ou como já dito por Paulo Freire fugir de uma “educação bancária”.

Destarte, como sempre, non sine aliquo metus escribo...por considerar que certamente cometerei alguns abusos e falhas, devido ao meu conhecimento ainda incipiente sobre o assunto.

Então para iniciar, creio ser pertinente esclarecer os conceito de escalar e vetor.

Escalar : são valores que para sua definição necessitam somente de uma grandeza para caracteriza-los por exemplo : x quilos; x metros; x quilômetros; +/- x graus centígrados, e seu valor se exprime por meio de um número algébrico ou relativo, isto é, depende do sinal, que tanto pode ser positivo quanto negativo ou seja, não possuem sentido ou direção..

Vetor

O conceito de vetor surgiu de forma embrionária com o matemático e engenheiro flamengo

Stevin – o Arquimedes holandês – No seu trabalho “Estática e Hidrostática”, publicado em 1586, ele apresentou o problema da composição de forças e instituiu uma regra empírica para se

determinar a soma ou resultante de duas forças aplicadas em um mesmo ponto.

Tal regra é conhecida nos dias atuais como regra do paralelogramo.

                                       

Onde:

a) Escolhe-se um ponto qualquer (ponto P).

b)Coloca-se a origem dos dois vetores nesse ponto.

c)Completa-se o paralelogramo usando linhas imaginárias.(no caso, as linhas não segmentadas)

d)O vetor resultante tem origem no ponto P e tem a mesma direção da diagonal que parte de P.

No entanto, quem primeiro apresentou um método para tratar grandezas vetoriais, por intermédio da Álgebra Escalar, foi Descartes.

O método consistia na decomposição de tais grandezas em três componentes. A necessidade de um Cálculo que pudesse operar sobre vetores já era desde há muito sentida e, em 1679, Liebniz chamou a atenção para o fato, embora sem muito sucesso.

O problema atraiu a atenção de pensadores que se seguiram, mas somente bem mais tarde, em 1879, os vetores aparecem como sendo linhas dirigidas – que hoje são conhecidos como segmentos orientados – na obra “Ensaio Sobre a Representação da Direção”, de Wessel.

Especificamente, vetores: são valores que necessitam para sua definição, direção e sentido, por exemplo, grandeza como : Aceleração, pois, ao referirmo-nos à ela temos que assinalar uma direção, e um sentido como no caso da aceleração da gravidade ou na aplicação de uma Força, também somos forçados a informar, qual é a direção e o sentido de aplicação das mesmas.

Espaços vetoriais e vetores

Na álgebra linear, um espaço vetorial (ou o espaço linear) é uma coleção dos objetos abstratos (chamados vetores) que possuem algumas propriedades que valem serem estudadas, dito isto, podemos dizer que se tivermos um conjunto de vetores formaremos o que chamamos de espaço vetorial, no qual podem ser realizadas as operações como soma, subtração, decomposição e multiplicação de vetores.

Aqui neste espaço de forma sucinta, importa saber que tais objetos (vetores) podem ser adicionados uns aos outros e multiplicados por um número escalar.

O resultado dessas operações é sempre um vetor pertencente ao mesmo espaço.

Vale enfatizar que os espaços vetoriais são os objetos básicos do estudo na álgebra linear, e têm várias aplicações na matemática, na ciência, e na engenharia.

O espaço vetorial mais simples e familiar é o espaço Euclidiano bidimensional. Os vetores neste espaço são pares ordenados e são representados graficamente como "setas" dotadas de módulo,

                                

direção e sentido.

No caso do espaço euclidiano bidimensional, a soma de dois vetores quaisquer pode ser realizada utilizando a regra do paralelogramo, conforme mencionada acima, ou a lei dos Cossenos aplicando a formula:

                                      

 em vetores com direções obliquas, onde  é o ângulo entre as direções dos dois vetores.

Todos os vetores também podem ser multiplicados por um escalar - que no espaço Euclidiano é sempre um número real.

Esta multiplicação por escalar poderá alterar o módulo do vetor e seu sentido, mas preservará sua direção.

O comportamento de vetores geométricos sob estas operações fornece um bom modelo intuitivo para o comportamento dos vetores em espaços mais abstratos, que não precisam ter a mesma interpretação geométrica.

Como exemplo, é possível citar o espaço de Hilbert (onde "habitam" os vetores da mecânica quântica) e dizer informalmente que tal espaço se trata de um espaço vetorial completo, onde os possíveis estados de um sistema físico são representados por vetores.

Sendo ele também um espaço vetorial, é certo que possui propriedades análogas àquelas do espaço Euclidiano.

Etimologicamente a palavra vetor provém do verbo latino vehere, que significa transportar, levar.

Neste espaço mencionado, os vetores carregam informação sobre o quê?

Claro que em nosso caso, é sobre o chamado qubit, pois, assim como há na computação clássica o bit que é a menor unidade de informação e é representado por [0] e [1], na computação quântica o bit transforma-se em qubit ou comumente como é chamado quantum bit, ou abreviadamente qubit.

Porém, a grande diferença entre os bits clássicos e os qubits é que o bit clássico pode estar somente com um valor armazenado num determinado instante, esse valor é 0 ou 1. O bit quântico (qubit) está numa superposição de 0’s e 1’s num determinado instante, ou seja, 0 e 1 estão armazenados ao

                                        

mesmo tempo, vemos acima, como representação genérica a fórmula do par de qubits.

Porém, o bit quântico refere-se ao [0] ao [1], com a denominação de estado e a representação desse estado em forma de um vetor, cujo símbolo é | 0 > , vale dizer, que o valor interno ao símbolo | > na sua forma genérica pode ser {x.,y, z, 0, 1 ,2 ..etc}. Assim temos , sendo que o simbolo fi representa o estado de um qubit..

E este conjunto de símbolos na notação de Dirac é denominado Ket.

Por ser uma forma dual de representação, existe a forma oposta que é denominada Bra, e o símbolo correspondente é < 0 | , frisando que para o valor interno vale o que foi dito para o Ket.

Esses símbolos obedecem às regras algébricas pertinentes ao campo dos vetores e há alguns postulados definidos para a notação de Dirac.

Por exemplo:

a) O principio da superposição.

b) A interpretação da função de onda.

c) Tratamento dos observáveis.

d) Princípio da correspondência.

e) Tratamento da Equação e Schrödinger.

Algumas definições

Uma expressão do tipo  bra por um vetor ket, como na operação de produto escalar entre dois vetores.
  é um produto escalar de um vetor

Por exemplo, se tivermos a operação do vetor | A.| ² = 1 podemos representá-la pelo símbolos ket |A> e o símbolo bra <A| que formam a operação <A|A> = 1, pois neste caso, A é um vetor unitário.

Agora na operação entre dois vetores diferentes no caso entre os vetores A e o vetor B teremos, <A|B> = 0, em função de serem vetores ortonormais entre si.

Uma boa forma de representação gráfica dos vetores é feita pela esfera de Bloch, que proporciona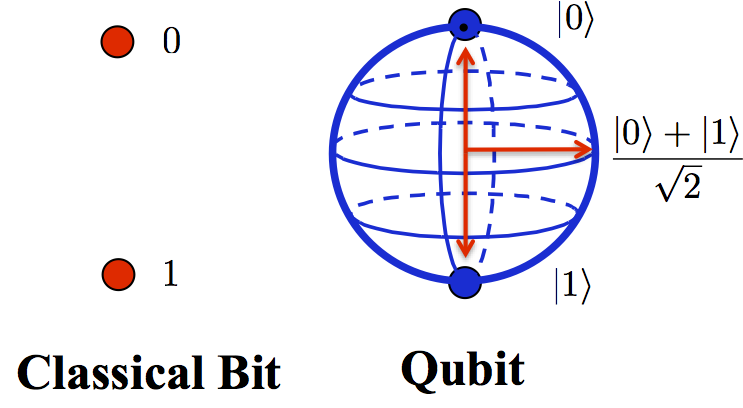

                              

                                                    Esfera de Bloch
uma interpretação mais intuitiva dos vetores e dos qubits no espaço.

E a representação genérica dos qubit é também nós podemos expressar genericamente o estado de um qubit como , onde os ângulos e definem um

ponto na esfera, então podemos inferir que todas as transformações que ocorrem num qubit são na verdade rotações do vetor na esfera de Bloch.

                        

Além do controle e da manipulação individual de átomos e moléculas, os pesquisadores da área de informação quântica já produzem um dos fenômenos mais intrigantes da natureza: os chamados estados emaranhados de fótons (ou ‘fótons gêmeos’).

Fótons gêmeos são produzidos quando se ilumina um cristal com um feixe de laser intenso. Existe uma certa probabilidade, que aumenta com a intensidade do laser, de que cada fóton do feixe incidente seja absorvido pelo cristal, ao mesmo tempo em que é produzido um par de fótons. 

Depois de formados, esses pares passam a ter suas propriedades fortemente correlacionadas, ou seja, qualquer medida efetuada em um deles altera as propriedades do outro, mesmo que o par esteja separado por milhares de quilômetros. 

Daí o nome de ‘fótons gêmeos’ para esses pares emaranhados.

Einstein chegou a dizer que entre dois fótons emaranhados agia “uma fantasmagórica ação à distância”. ( spooky action at a distance – nota do blog )

Porém, no início da década de 1980, foi mostrado experimentalmente que essa ‘estranha’

correlação existia de fato entre partículas gêmeas.

Hoje, as propriedades desses estados emaranhados têm levado a aplicações em computação quântica e a demonstrações de novos processos quânticos, como o teletransporte.

Os estados emaranhados de fótons permitem uma nova forma de comunicação, baseada no envio de informação completa sobre o estado quântico de um sistema de um lugar para outro. Isso é notável, pois, para um único sistema quântico, já sabemos que não é possível medir seu estado quântico. Porém, é possível transmiti-lo, usando, para isso, um canal de comunicação quântico, formado por dois fótons gêmeos.( CIÊNCIA HOJE • vol. 35 • nº 206) destaques de minha autoria.

Entrelaçamento - Emaranhamento - Entanglement
O primeiro passo para entender o comportamento do entrelaçamento é identificar quando um estado quântico composto possui entrelaçamento ou não, isto é, determinar regras (critérios) para saber se esse estado quântico é ou não entrelaçado.
Feito esse estudo, surge a necessidade de quantificar o entrelaçamento, isto é, determinar o quão entrelaçado tal estado quântico é.
Os estados quânticos compostos mais simples, onde há possibilidade de algum entrelaçamento ser detectado, são os estados quânticos de sistemas de dois qubits. 
São exatamente nesses estados onde foram concentrados os primeiros esforços na tentativa de quantificar o entrelaçamento. 
Por isso, a maior parte dos critérios e medidas de entrelaçamento existentes se refere a estados de sistemas de dois qubits. Como conseqüência dessa investigação surgiram alguns critérios e medidas de entrelaçamento para estados bipartes de dimensões arbitrárias. (JOÃO LUZEILTON DE OLIVEIRA FERRAMENTAS ALGÉBRICAS PARA O ESTUDO DO ENTRELAÇAMENTO QUÂNTICO)
                                          

                                  
                                    dois qubits emaranhados

Estados entrelaçados. 

A configuração do spin singleto é o exemplo clássico de um estado entrelaçado - um estado de duas partículas que não pode ser expresso como produto de dois estados de uma partícula, e, para o qual, portanto, não se pode realmente falar do 'estado' de cada partícula separadamente.

Considere o estado de um sistema de dois qubits dados por   

Observe que este estado não pode ser representado como 

para quaisquer números complexos.

Não podemos analisar o estado individual de cada qubit neste sistema, porque os estados dos dois qubits estão emaranhados.

Se nós efetuarmos uma medida sobre o primeiro qubit, então o estado do outro qubit é determinado pelo resultado da medida.

Por exemplo, com a probabilidade 1 / 2 nós vemos

como resultado de uma medida, e neste caso, nós saberemos que o estado do sistema deve ser

Estados emaranhados fornecem um método de apresentação, no qual os resultados da mecânica quântica não podem ser explicados por nenhuma teoria de “variáveis ocultas” ou  

( spooky action at a distance ).

Assim, estados que não podem ser decompostos em produtos tensoriais são chamados estados emaranhados.

Também, vale dizer que a palavra teletransporte ou teleporte é usada em ficção científica para descrever o processo de mover objetos de um ambiente a outro codificando informação sobre os objetos, transmitindo esta informação a outro local e depois criando uma cópia dos objetos originais no novo local.

O teletransporte quântico possui este nome porque ele possui estas características em comum com a noção fictícia de teletransporte:

1. bits quânticos são codificados como bits clássicos;
2. a informação a ser transmitida é destruída durante o processo (devido a observação); e

c) o qubit transmitido é reconstruído a partir dos bits clássicos e do par EPR.

  
Uso do quBit na Computação Quântica


                       

                                 O primeiro processador quântico funcional
Aplicações práticas
Um dos primeiros compradores do computador quântico da D-Wave foi a gigante Lockheed Martin, uma das principais representantes da indústria bélica dos Estados Unidos. 
Lá, a máquina auxilia no cálculo de operações que iriam requerer um grande número de tentativas e permutações, agilizando muito os resultados. 
Uma equipe da Universidade de Harvard conseguiu utilizar o D-Wave One para prever as configurações de mais baixa energia de uma proteína dobrada. 
Desvendar o processo de dobramento de proteínas é um dos maiores anseios de todos os pesquisadores das chamadas biociências, médicos incluídos, porque isso pode significar a descoberta de formas totalmente novas de lidar com a fisiologia humana.
O problema é que as proteínas são muito complexas, e são inúmeras as formas possíveis que elas podem assumir em seu dobramento. Sendo assim, o computador quântico não resolveu "toda" a questão do dobramento das proteínas, tendo ele trabalhado com alguns poucos aminoácidos. Mas o objetivo do teste era mostrar que um computador quântico pode lidar com esse tipo de problema. Algumas teorias apontam que os computadores quânticos são muito melhores adaptados para a tarefa do que os computadores eletrônicos clássicos, embora houvesse discordâncias quanto a isso. No lado positivo, o processador quântico da D-Wave identificou as configurações de aminoácidos e suas interações correspondentes àquilo que seria o meio mais "econômico" do dobramento das proteínas. No lado negativo, ele acertou 13 vezes em 10.000 medições. (http://www.comppet.ufu.br/printf/?q=content/o-que-existe-dentro-de-um-processador-qu%C3%A2ntico)

Utilizando parte das considerações finais do livro Física Moderna II de Ana Paula Andrade, encerro.

[..] Apesar dos muitos questionamentos e oposição, a mecânica quântica é hoje uma das mais importantes e bem sucedidas teorias científicas.

Como prova desta afirmação, está o fato de que a maior parte dos laureados com o prêmio Nobel de Física no século XX corresponde a trabalhos teóricos e experimentais na área de física quântica.

Por certo que o avanço científico alcançado nesta área possibilitou o desenvolvimento de muitos dispositivos eletrônicos que operam na escala dos fenômenos quânticos, a exemplo das ferramentas de nanotecnologia.

Aplicações de conceitos quânticos se estendem desde a medicina à informática. Lasers, semicondutores, equipamentos de ressonância magnética e microscópio eletrônico são apenas algumas, dentre muitas outras aplicações.

Atualmente, muito esforço vem sendo realizado na investigação das manipulações quânticas, a fim de desenvolver um sistema de criptografia quântica, conceito por trás do funcionamento de computadores quânticos.”

                           

ttp://pt.wikipedia.org/wiki/Bit_qu%C3%A2ntico

https://www.youtube.com/watch?v=XMk6WuAmsKk
https://www.youtube.com/watch?v=q5Uy0Or2_6g (Teletransporte)

Quantum entanglement (emaranhamento)

Quantum Theory It"s Unreal

Introduction to Quantum Computers